Masterstudium Computational Science and Engineering
- Studienkennzahl
-
UE 066 646 - Masterstudium Computational Science and Engineering
- Studiendauer
-
4 Semester
- Umfang
-
120 ECTS
- Sprache
-
Englisch
- Abschluss
-
Master of Science (MSc)
- Studienplan
- Curriculum
Studieninhalte
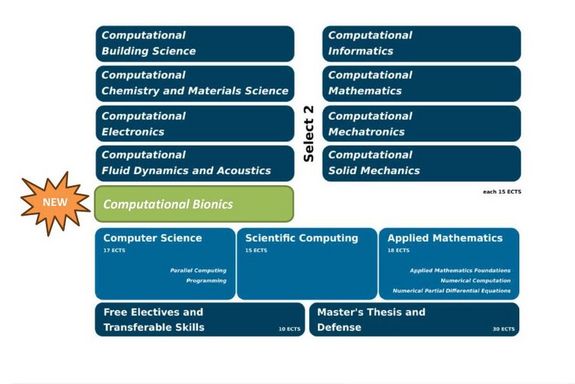
Das Masterstudium Computational Science and Engineering vermittelt Grundlagenwissen im Bereich der angewandten Mathematik und Informatik und ermöglicht eine Schwerpunktsetzung über mindestens zwei Prüfungsfächer als Schlüsselbereiche aus einem fakultätsübergreifenden Katalog (alphabetisch geordnet): Computational Bionics (ab Wintersemester 2024), Computational Building Science, Computational Chemistry and Material Science, Computational Electronics, Computational Fluid Dynamics and Acoustics, Computational Informatics, Computational Mathematics, Computational Mechatronics, Computational Solid Mechanics. Jedes dieser Wahlmodule ist aufgebaut aus (verpflichtenden und) optionalen Lehrveranstaltungen. Dies ermöglicht sowohl eine Angleichung des Ausbildungsniveaus als auch eine flexible Anpassung an die Interessen und Stärken der jeweiligen Studierenden.
Weitere Informationen zum Studium
Der stetige Fortschritt in Wissenschaft und Technik ist zunehmend von rechenintensiven Computersimulationen abhängig. Aus der Notwendigkeit heraus diese Computersimulationen präzise und schnell durchführen zu müssen, hat sich Computational Science and Engineering als eigenständiger und interdisziplinärer Forschungsbereich international herauskristallisiert. Dieser verbindet insbesondere die numerische Mathematik und Informatik mit Naturwissenschaften und Technik, um effiziente Computersimulationen in einer Vielzahl von Anwendungen im Bereich Bauingenieurwesen, Chemie, Elektrotechnik, Maschinenbau, Materialwissenschaften, Mechatronik und Physik unter Einsatz von hoch parallelisierten Computersystemen – von einzelnen Workstations bis hin zu großen Rechenclustern und Supercomputern – zu ermöglichen.
Das englischsprachige Masterstudium Computational Science and Engineering vermittelt die dafür notwendigen interdisziplinären sowie wissenschaftlichen und exzellenten fachlichen Kompetenzen.
Das Masterstudium Computational Science and Engineering richtet sich an Absolventinnen und Absolventen eines naturwissenschaftlichen oder technischen Bachelorstudiums. Bewerberinnen und Bewerber sollen ein starkes Interesse an der Entwicklung und Durchführung von Computersimulationen haben. Dem zu Grunde soll eine Begeisterung an der Entwicklung von effizienten Programmcodes für die angewandte Mathematik sowie für die physikalische Modellierung komplexer Systeme liegen.
Das Masterstudium Computational Science and Engineering ist prinzipiell für Absolventinnen und Absolventen eines naturwissenschaftlichen oder technischen Bachelorstudiums geeignet.
Automatisch zur Zulassung ohne Auflagen sind Absolventinnen und Absolventen bestimmter Bachelorstudien der TU Wien berechtigt (siehe: Details Zulassungsvoraussetzungen). Im Falle eines anderen Studienabschusses müssen im Vorstudium Lehrveranstaltungen in Ausmaß von insgesamt zumindest 30 ECTS in den Bereichen Informatik und Mathematik absolviert worden sein.
Für Fragen zur Antragstellung und Studien, öffnet in einem neuen Fensterzulassung, öffnet in einem neuen Fenster wenden Sie sich bitte an die Studienabteilung.
Personen, deren Muttersprache nicht Englisch ist, haben die Kenntnis der englischen Sprache nachzuweisen. Für einen erfolgreichen Studienfortgang werden Englischkenntnisse nach Referenzniveau B2 (entspricht österreichischem Maturaniveau) des Gemeinsamen Europäischen Referenzrahmens für Sprachen empfohlen. Manche ergänzenden Lehrveranstaltungen zur Erlangung der vollen Gleichwertigkeit des absolvierten Studiums werden auf Deutsch angeboten. Daher werden Deutschkenntnisse nach Referenzniveau B1 des Gemeinsamen Europäischen Referenzrahmens für Sprachen empfohlen.
Es gibt keine formalen Einschränkungen dazu, in welcher Reihenfolge Lehrveranstaltungen (LVAs) zu absolvieren sind, prinzipiell ist die Semesterplanung den Studierenden also frei überlassen. Aufgrund des aufbauenden Charakter des Studium ist es jedoch ratsam, den Empfehlungen zur Semesterplanung zu folgen.
Neben Empfehlungen dazu, welchen Semestern die LVAs der Pflichtfächer und Basismodule sowie der Schlüsselbereiche absolviert werden sollten, finden Sie dort auch Empfehlungen zum Studienbeginn im Sommersemester: Zwar ist die Zulassung sowohl im Winter- als im Sommersemester möglich, die meisten LVAs werden jedoch nur in einem von beiden angeboten. Daher und aufgrund des aufbauenden Charakters des Studiums, ist der Beginn im Wintersemester von Vorteil für die Abfolge Ihrer gewählten Kurse.
Als Ergänzung zu den Lehrveranstaltungen der Pflichtfächer und Schüsselbereiche sind 10 ECTS für das Modul Freie Wahlfächer und Transferable Skills zu absolvieren. Davon sind zumindest 4,5 ECTS an Lehrveranstaltungen aus dem zentralen Wahlfachkatalog Transferabel Skills, öffnet eine externe URL in einem neuen Fenster zu wählen.
Folgende Lehrveranstaltungen werden darüber hinaus zur Absolvierung im Modul empfohlen:
- 057.020 VSC-School I Kurse zum Thema Hochleistungsrechnen (Wintersemester)
- 057.021 VSC-School II Kurse zum Thema Hochleistungsrechnen (Sommersemester)
- 040.003 Wissenschaftliches Arbeiten: Recherchieren, Zitieren, Schreiben (Wintersemester)
- 040.004 Scientific Work: Publishing and Dissemination (Wintersemester)
Detaillierte Antworten zu den geläufigen Fragen rund um das Masterstudium Computational Science and Engineering (betreffend Abhaltemodus, Programmiersprachen, Schlüsselbereiche, Anerkennung von Prüfungen, Diplomarbeit, Doktoratsstudium und Jobaussichten) finden Sie auf der Seite Frequently Asked Questions.
Prüfungsfächer und Module
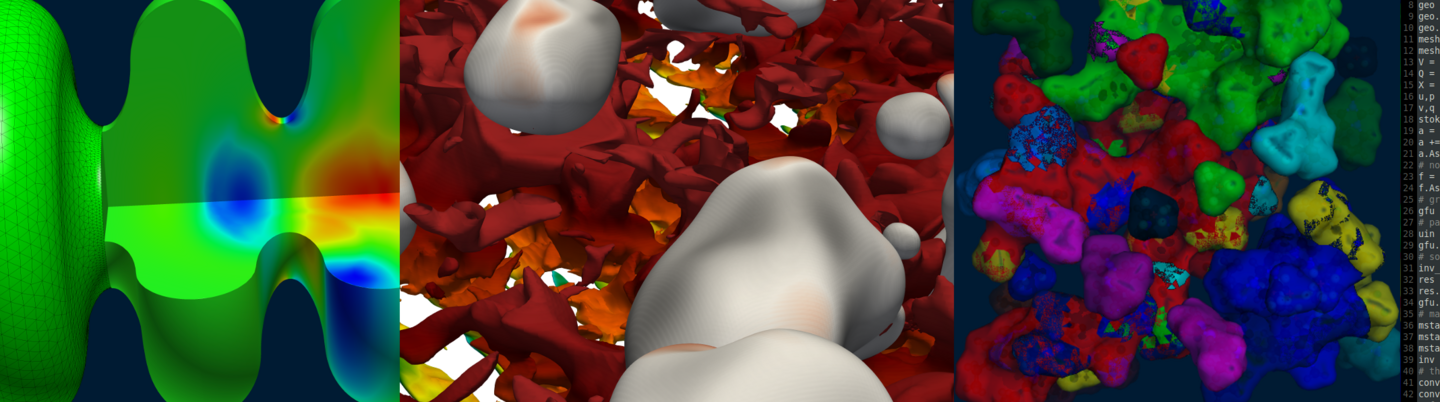
Anwendungsbeispiele

Micro-Plate
Andre Gesing ist Autor des Bildes und es zeigt den Flow um eine Micro-Plate. Weite Infos von Daniel Platz.
Stent Animation
Geometrieaufbau einer Stent-Geometrie.