Quantum Criticality – The Puzzle of Multiple Energy Scales
Host Institution: TU Wien, opens an external URL in a new window
Project duration: 1 June 2009 - 31 May 2015
Matter at the absolute zero in temperature may reach a highly exotic state: Where two distinctly different ground states are separated by a second order phase transition the system is far from being frozen; it is undecided in which state to be and therefore undergoes strong collective quantum fluctuations. Quantum criticality describes these fluctuations and their extension to finite temperature. Quantum critical behavior has been reported in systems as distinct as high-temperature superconductors, metamagnets, multilayerHe films, or heavy fermion compounds. The latter have emerged as prototypical systems in the past few years. A major puzzle represents the recent discovery of a new energy scale in one such system, that vanishes at the quantum critical point and is in addition to the second-order phase transition scale that governs the behavior of conventional quantum critical points. Completely new theoretical approaches are called for to describe this situation.
In this project we want to explore the nature of this new low-lying energy scale by approaches that go significantly beyond the state-of-the-art: apply multiple extreme conditions in temperature, magnetic field, and pressure, use ultra-low temperatures in a nuclear demagnetization cryostat, and perform ultra-low energy spectroscopy, to study carefully selected known and newly discovered heavy fermion compounds. Samples of outstanding quality, in both bulk and thin film form, will be prepared and characterized within the project and, in some cases, be obtained from external collaborators. New approaches in the theoretical description of quantum criticality will accompany the experimental investigations. The results are likely to drastically advance not only the fields of heavy fermion systems and quantum criticality but also the current understanding of phase transitions in general which is of great importance far beyond the borders of condensed matter physics.
The ERC Project
The pressing open problems to be addressed include:
- Can one determine the analog of Figure 2 (see Background), i.e. highly reliable universal scaling curves for unconventional quantum criticality?
- What is the microscopic meaning of the new energy scale in heavy fermion compounds?
- Is the appearance of additional energy scales universal for unconventional quantum criticality or are there different kinds hereof?
- Can the local quantum criticality scenario be combined with powerful band structure methods to obtain quantitative agreement with experiments?
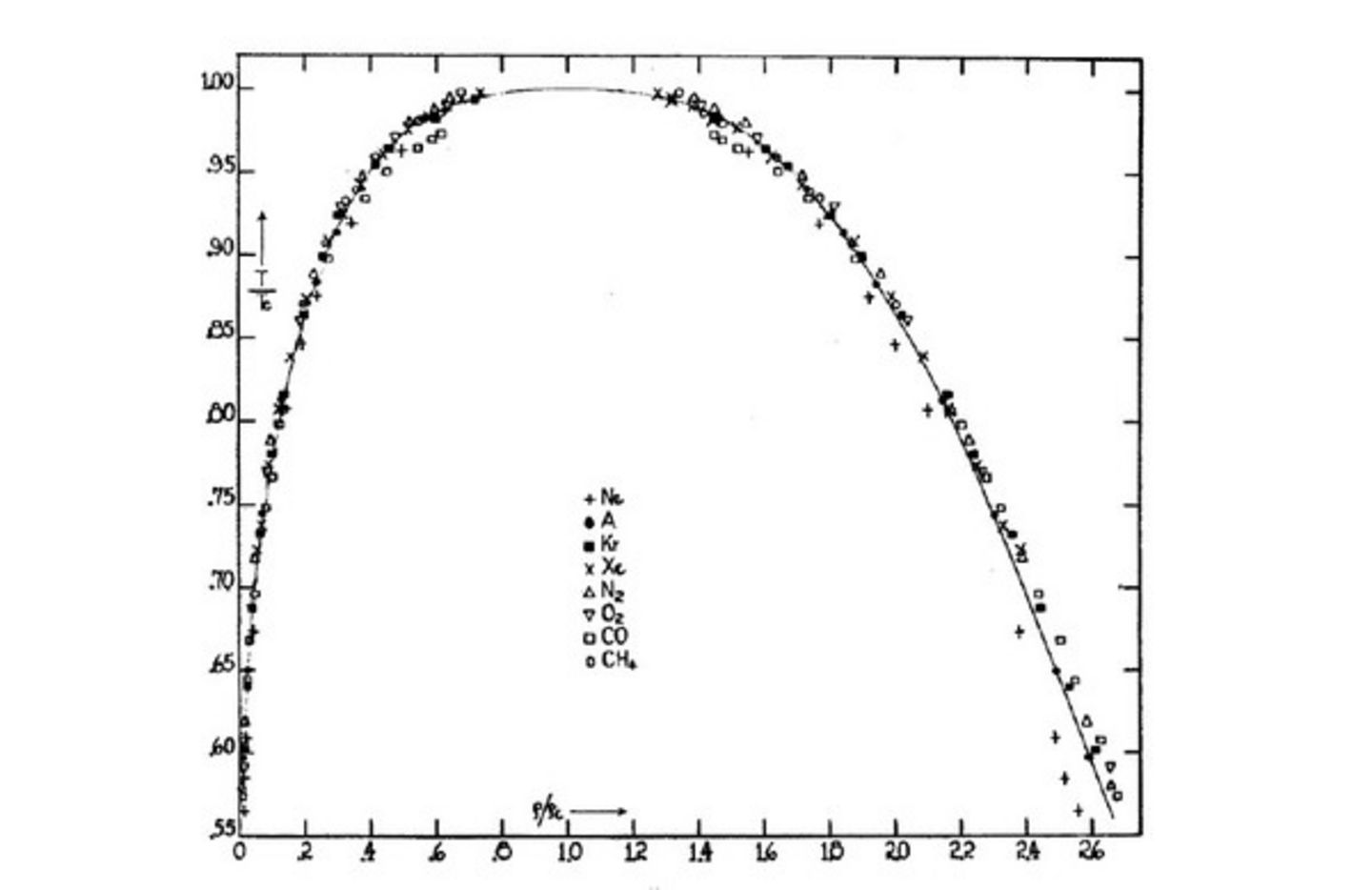
Universal scaling in the liquid gas transition for eight different liquids. After E. A. Guggenheim, J. Chem. Phys. 13, 253 (1945).
We will attempt to answer these questions using a multifaceted approach, as illustrated below. The different facets are represented as pieces of a jigsaw “quantum puzzle”. It needs to be fully assembled to find the solutions – a new level of understanding of unconventional quantum criticality in heavy fermion compounds and, more generally, of phase transitions in matter.
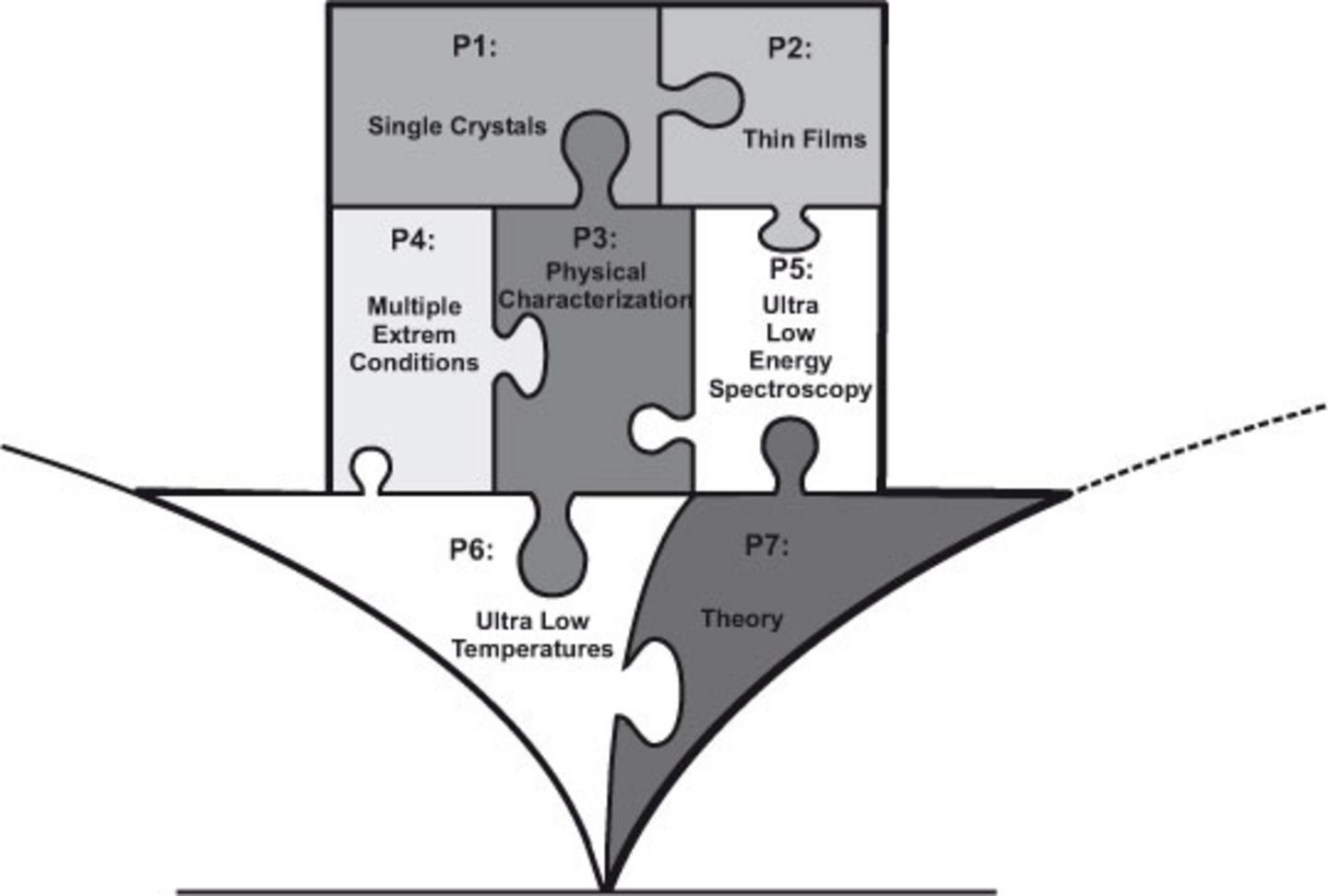
QuantumPuzzle: Schematic representation of the tasks as pieces of a jigsaw "quantum puzzle".
Pieces P1 and P2 define the materials basis where highest quality samples are prepared both in “bulk” and thin film form. To push sample quality on the bulk side (P1) to extremes, the institut's state-of-the-art crystal growth infrastructure will be supplemented with carefully selected new equipment. An important task of P1 is, besides the growth of highest-quality single crystals of known compounds, to search for new materials which display unconventional quantum criticality. This is very important since to date unconventional quantum criticality has been observed only in a relatively small number of compounds. Also the number of clear-cut SDW transitions is not large.
Thin film techniques (P2) provide additional parameters (e.g. choice of substrate) to deliberately taylor a given compound. This will be exploited in the project to tune the distance of compounds to their quantum critical point. In addition thin films will, for nothing but their reduced weight and dimension, be needed for some of the experiments described below. Excellent scientific and technical support is provided by the Center for Micro- and Nanostructures (ZMNS) at TU Wien. A new molecular beam epitaxy (MBE) chamber will shortly be available for QuantumPuzzle at the ZMNS.
A broad physical characterization of the materials produced in P1 and P2 will follow in P3, using state-of-the-art techniques available at the institute and large facilities such as ILL (neutrons) or PSI (muons). The goal is to identify by these experiments the samples most promising for the highly advanced measurements in P4-6.
Experiments to be conducted in P4 go beyond state-of-the-art. While in most heavy fermion compounds the variation of one external “tuning” parameter suffices to drive a material to quantum criticality (e.g. magnetic field in the case of Figure 1), others need to be simultaneously subject to two or more extreme conditions. As an example, in the case of CeRhIn5, one of the most promising candidates for unconventional quantum criticality, these conditions are high pressure, high magnetic field, and low temperatures.
Another experimental jigsaw piece, P5, focusses on key question 2, the nature of the new energy scale. With a radically new approach of ultra low energy spectroscopy, employing technical know-how from the superconducting quantum bits community, we will attempt to “optically” excite the new energy scale. We expect a clear-cut answer on whether or not this scale represents the suspected breakup of the heavy quasiparticles.
While the above pieces mostly focus on key questions 2 and 3, the approach of P6, going to ultra-low temperatures, is at the heart of question 1: To test for universal scaling, accurate temperature dependences of both thermodynamic and transport properties are needed in the widest possible temperature range. By using a nuclear demagnetization cryostat which will be shortly installed at IFP we aim at going 1 to 2 orders of magnitude below the temperatures typically reached to date in investigations of quantum criticality in heavy fermion compounds.
All important advance in the field of quantum criticality have come about by intense collaboration between theoreticians and experimentalists in the field. This successful approach shall also be used in QuantumPuzzle (P7). Focus will be on introducing material specific aspects into the calculations, e.g. by using LDA + DMFT.
Physics of Quantum Criticality
Quantum criticality is at the forefront of modern condensed matter physics. The recent discovery of an entirely unexpected energy scale [S. Paschen et al., Nature 432, 881 (2004), P. Gegenwart et al., Science 315, 969 (2007); see Fig. 1] in the phase diagram of a prototypical quantum critical compound mystified the community. With our project QuantumPuzzle we address the key issues of this discovery and set out to solve the “quantum puzzle” with techniques that go drastically beyond the state-of-the-art in the field.
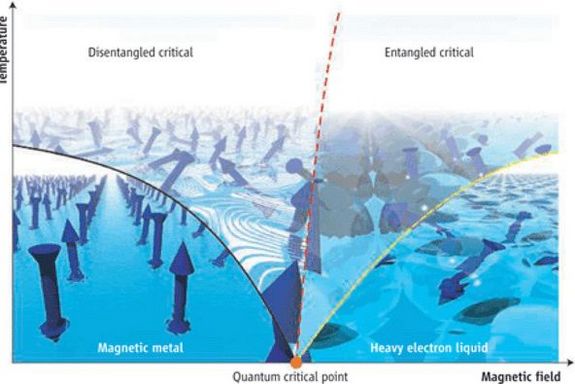
Figure 1: The quantum critical point (QCP) in YbRh2Si2. The horizontal axis gives the magnetic field that allows to tune through the transition. The vertical axis denotes temperature. The black and yellow lines (to left and right of the QCP, respectively) are related to the correlation length via the traditional theory of quantum criticality. The additional crossover line (in red/towards top) is unanticipated by the traditional theory. From A. Schofield, Science 315, 945 (2007).
The three different phases of water, the solid, liquid, and gas phase are familiar to most of us and early childhood experience taught us that the ambient temperature ultimately determines the phase water will be in. It is obvious that phase changes must be collective phenomena involving many particles. After all, a single water molecule is not a gas nor a liquid and certainly not a solid. Modern condensed matter relates the solid character of ice (i.e. the rigidity) to the periodic alignment of the water molecules in ice. This periodicity is in fact a characteristic feature of all solids that gives rise to specific patterns in X-ray scattering experiments. The rigidity emerges when liquid undergoes a phase transition to the solid state. While the strength of this rigidity is a material specific quantity (the shear modulus), its mere existence is tied to general symmetry arguments.
As it turns out, there are two broad classes of phase transitions: continuous or discontinuous ones. Discontinuous transitions are sometimes called first order transitions. Quantities which are related to the emerging order, so-called generalized susceptibilities, diverge at continuous transitions because they directly probe the amount of fluctuation in the associated quantity. The existence of fluctuations on all length scales right at the transition is the characteristic feature of a continuous phase transition and is commonly referred to as criticality. As the temperature is tuned towards the so-called critical temperature, the length scale on which fluctuations occur tends towards infinity and gives rise to universal behavior.

Universal scaling in the liquid gas transition for eight different liquids. After E. A. Guggenheim, J. Chem. Phys. 13, 253 (1945).
Figure 2 shows an example of universality for the liquid to gas transition and is one of the earliest scaling plots. Different liquids are described by the same hence universal scaling curve near their respective continuous transition (Tc and pc denotes the critical temperature and pressure, respectively). The universal scaling curve is a reflection of the fact that the approach to the critical point is characterized by the vanishing of a single length scale. In fact, this physical behavior is so universal across different systems that the scaling curves will only depend on very general properties like, e.g. the symmetry properties of the emerging order or the space dimensionality. As a result, even the continuous transition from a normal metal to a ferromagnet is described by a scaling curve identical to the one in Figure 2. As Figure 2 already suggests, the transition can be reached by either fixing the ambient pressure to the critical pressure and then tuning the temperature through its critical value or by setting the temperature to the critical value and addressing the phase transition as a function of pressure.
If the transition happens to occur at zero temperature, it is customary to call it a quantum phase transition. This alludes to the fact that only in this case quantum mechanical fluctuations can successfully conspire with thermal fluctuations and modify the scenario outlined so far. Since the transition occurs at zero temperature, a different – non-thermal – control parameter is needed to tune through the transition. Depending on the particular system under consideration this tuning parameter may be, for example, pressure, magnetic field, or a sequence of different materials that differ in a well-controlled manner. The materials that are central to our proposal are compounds complex enough to – at least in certain cases – enable tuning across a quantum phase transition by changing the mass relationships among elements that constitute the compounds. This is called stoichiometric tuning. Again, the transition may be continuous or discontinuous in close analogy to the classical case outlined above.
The overall picture that so far has emerged for quantum phase transitions by and large parallels that of classical phase transitions. The most prominent modification comes from a change in the effective spatial dimension that should be used to describe the universal scaling behavior. The approach to a continuous quantum phase transition should therefore be characterized by the vanishing of one length or energy scale, which we will refer to as the correlation length.
The recent discovery of a heavy fermion compound whose approach to quantum criticality is characterized by at least two independent energy scales is the motivation for our project QuantumPuzzle. With the general state of affairs in mind it becomes clear that the mere existence of such additional scales, independent from the scale set by the correlation length, poses a severe challenge to our understanding. It is to be expected that the resolution to this problem will not only have ramifications to the general theory of quantum phase transitions but also to our understanding of emergent quantum phases in complex materials.
Ordinary metals, e.g. aluminum, are well described in terms of a Landau Fermi liquid. Electrons in such a Fermi liquid are completely independent of each other except for an adjustment in certain parameters like the electron mass. This in itself is truly remarkable, given that electrons carry charge and therefore should repel each other. This feature is a consequence of the quantum mechanical delocalization of the electron across the metal. More precisely, the fundamental particle in a metal like aluminum is an excitation that carries the charge of an electron but is a quasi-particle to which many electrons contribute as the enhanced effective mass indicates.
In heavy fermion systems two different kinds of electrons determine the physical properties. Heavy fermion systems contain delocalized electrons just like aluminum, but, in addition, contain localized electrons that all by themselves would not carry an electric current. An intricate many body effect, called the Kondo effect, nonetheless allows the localized electrons to contribute to the electronic properties by forming a quasi-particle with the delocalized electrons. The Kondo effect thus entangles the localized electrons with the delocalized ones. The resulting quasi-particles in a heavy fermion compound form a Fermi liquid that typically has an effective mass that exceeds the bare electron mass by a factor of up to 1000.
In the conventional approach to quantum criticality, the Fermi liquid may undergo a quantum phase transition to a magnetically ordered state. This is called the spin density wave scenario (SDW). Figure 1 shows the phase diagram of YbRh2Si2. The quantum critical point is accessed through magnetic field tuning. For magnetic fields larger than the critical field, YbRh2Si2 is in a heavy fermion state. For field strength below the critical field the compound orders magnetically. Both the black and yellow lines (to left and right from the quantum critical point, respectively) are related to the correlation length via the traditional theory of quantum criticality.
The puzzling feature unaccounted for by the traditional theory is the crossover region (red line towards top) that vanishes at the QCP. Several alternatives and modifications of the SDW scenario have been put forth. One of the promising alternatives is called local quantum criticality. It predicts a completely new form of quantum criticality where the heavy quasiparticles break up concomitant with the onset of magnetic ordering. Within this picture, the additional scale at the quantum transition is naturally explained as a consequence of the critically destroyed Kondo effect, as suggested in Figure 1.
