Stellen Sie sich vor, Sie müssen eine große Anzahl von Leuten besuchen, die zufällig verstreut an verschiedenen Orten wohnen. In welcher Reihenfolge steuert man die Reiseziele an, um insgesamt einen möglichst kurzen Weg zu haben? Diese Fragestellung ist in der Informatik als „Problem des Handlungsreisenden“ bekannt. Die Lösung ist schwer zu finden: Man muss am Computer eine gewaltige Anzahl möglicher Weg-Kombinationen durchprobieren, um den kürzesten Pfad auswählen zu können. Es ist daher ein Beispiel für ein schwieriges Rechenproblem – ein „NP-schweres Problem“, wie man in der Informatik sagt. Der strikte Trennstrich zwischen „einfachen“ und „schweren“ Problemen, den man seit den Siebzigerjahren zieht, beginnt aber heute an Bedeutung zu verlieren: Professor Stefan Szeider vom Institut für Informationssysteme untersucht, warum es Rechenprobleme gibt, die sich in der Praxis lösen lassen, obwohl das nach einfachen Abschätzungen der klassischen Komplexitätstheorie eigentlich hoffnungslos aufwändig sein müsste.
Schwierige und leichte Probleme
Ein Beispiel für ein einfaches Problem ist das Zusammenzählen einer Liste von Zahlen. Für eine doppelt so lange Liste benötigt man doppelt so viel Rechenzeit – das ist überschaubar. Es handelt sich um ein Problem der Klasse „P“. (Die Rechenzeit wächst maximal mit einer bestimmten Potenz der Anzahl der Eingabedaten.) Schwierig wird es aber bei den sogenannten „NP-schweren Problemen“, bei denen die Anzahl der nötigen Rechenschritte mit allen bekannten Methoden zumindest exponentiell mit der Anzahl der Eingabedaten ansteigt. Das lässt sich beim Problem des Handlungsreisenden sehr klar sehen: Will man drei verschiedene Orte besuchen, gibt es sechs mögliche Reihenfolgen. Bei zehn Orten muss man schon über drei Millionen Möglichkeiten durchrechnen, und für siebzig Orte gibt es mehr mögliche Reiserouten als das Universum Atome hat. Sie alle durchzuprobieren ist völlig aussichtslos.
Frühe Begeisterung für Mathematik
Stefan Szeider interessierte sich schon früh für solche mathematisch-logischen Überlegungen. „Als Jugendlicher habe ich das berühmte Buch `Gödel-Escher-Bach‘ gelesen, in dem es um Logik und Gödels Unvollständigkeitssatz geht – von da an wollte ich unbedingt tiefer in dieses Thema einsteigen“, erzählt er. So wählte er an der Universität Wien die etwas exotische Studienrichtung „Formale Logik“ und schloss dann ein Mathematik-Doktorat ab. Danach führte sein Weg nach Kanada, an die Universität von Toronto. Dort arbeitete er in der Gruppe von Prof. Stephen Cook, der für seine wichtigen Beiträge zur klassischen Komplexitätstheorie und der Theorie der NP-schweren Probleme 1982 den Turingpreis erhielt. Die Frage, in welcher Beziehung die Komplexitätsklassen P und NP zueinander stehen, wurde später zu einem der „Millennium-Probleme“ erklärt – sieben große Fragen der Mathematik, für dessen Lösung eine Million Dollar ausgeschrieben ist.
Es funktioniert – und keiner weiß warum
Viele der Rechenaufgaben, die für die Praxis von Bedeutung sind, fallen unglücklicherweise in die Klasse der NP-schweren Probleme. Und trotzdem gibt es erstaunlicherweise Computerprogramme, die selbst für solche aufwändigen Probleme in überschaubarer Zeit die richtige Lösung finden. Man kümmerte sich einfach nicht um die pessimistischen Vorhersagen der Theorie, sondern versuchte, möglichst kluge Problemlösungen zu programmieren – und das mit Erfolg. Es kam zu einem Auseinanderdriften der theoretischen und der praktischen Forschung. Lag die Komplexitätstheorie also jahrzehntelang falsch? „Die theoretische Forschung macht sich das Leben schwer, weil sie das Zusatzwissen ignoriert, das man normalerweise automatisch mit dabei hat“, erklärt Stefan Szeider. In der Praxis hat man es meist nicht mit völlig zufälligen, unstrukturierten Daten zu tun. Um beim Beispiel des Handlungsreisenden zu bleiben: Die Reiseziele sind niemals völlig zufällig über die Landkarte verteilt – vermutlich sind viele seiner Zielorte in einigen großen Städten konzentriert, und dazwischen gibt es nur einige wenige zusätzliche Punkte, die er ansteuern muss. Damit lässt sich das Gesamtproblem auf mehrere Teilprobleme reduzieren, die getrennt voneinander in relativ kurzer Zeit gelöst werden können. Ein gutes Computerprogramm kann in den Eingabedaten eine Struktur erkennen und zur Vereinfachung des Problems benützen. „Wir arbeiten mit einem neuen theoretischen Modell, das diese strukturellen Eigenschaften berücksichtigt. Damit können wir erklären, warum die Computerprogramme so schnell laufen“, erklärt Stefan Szeider, „ - das Millenium Problem verliert damit an Bedeutung.“
Von Kanada über England zurück nach Wien
Um solche Fragen zu erforschen, nahm Stefan Szeider eine Stelle in Durham (England) an, wo er fünf Jahre lang blieb. Dort gelang es ihm, einen begehrten ERC-Grant zu bekommen – und mit diesem Förderpreis in der Tasche machte er sich neuerlich auf die Suche nach einer anderen Arbeitsstätte. Diesmal zog es ihn in seine Heimatstadt Wien zurück, ans Institut für Informationssysteme der Fakultät für Informatik. „Hier in Wien ist die Logik in der Informatik in den letzten Jahren zu einem wichtigen Forschungsbereich ausgebaut geworden. Es gibt hier viele gute Leute und viele spannende Projekte“, meint Stefan Szeider. Doch nicht nur die Wissenschaft hat ihn motiviert, an die TU Wien zu kommen. Auch die Lebensqualität der Stadt Wien war für ihn und seine Frau ein wichtiges Argument. Eine Metropole wie Wien bietet Möglichkeiten, die man in einer Kleinstadt wie Durham sicher nicht hat – ob auch ausreichend viel Zeit bleibt, diese Möglichkeiten zu genießen, ist freilich eine ganz andere Frage. Mittlerweile hat Stefan Szeider auch einen kleinen Sohn, und zwischen Wissenschaft und Familienleben bleibt für andere schöne Dinge – etwa für Jazzkonzerte – nicht mehr besonders viel Freiraum. Doch wer es schafft, scheinbar unlösbare Computeraufgaben zu etwas Lösbarem zu machen, der wird wohl auch an dieser Herausforderung nicht scheitern.
Logik für uns alle
Die Logik hat die Mathematik des zwanzigsten Jahrhunderts ganz entscheidend geprägt – nun, im einundzwanzigsten Jahrhundert, ist sie dabei, auch die Informatik dramatisch zu beeinflussen. Erkenntnisse aus der Komplexitätstheorie sickern heute in Computerprogramme aus ganz angewandten Bereichen ein – von der medizinischen Diagnostik bis zum Erstellen von Terminplänen. Das ist nicht nur deshalb wichtig, weil wir mit effizienteren Computerprogrammen Zeit sparen wollen – es ist letztlich auch eine Umweltschutzfrage. „Wir ärgern uns über langsame Programme und wollen immer schnellere Computer – dabei vergessen wir oft, dass ineffiziente Computercodes auch unnötig Energie verbrauchen“, betont Szeider. Mathematische Probleme einfacher lösen zu können, spart also nicht nur Zeit, sondern auch Energie und CO2-Ausstoß. Wer Logik also für ein trockenes, rein theoretisches Fach hält, das auf unser wirkliches Leben keine Auswirkungen hat, der argumentiert ausgesprochen unlogisch.
Was heißt hier „unlösbar“?
Prof. Stefan Szeider im Portrait

1 von 3 Bildern oder Videos
Prof. Stefan Szeider
Prof. Stefan Szeider

1 von 3 Bildern oder Videos
Zufällige Eingabe für ein Computerprogramm - ohne erkennbare Struktur.
Zufällige Eingabe für ein Computerprogramm - ohne erkennbare Struktur.
1 von 3 Bildern oder Videos
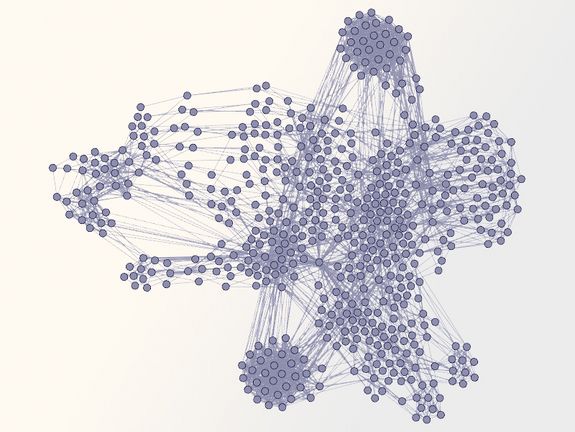
Reale Eingabe aus der Praxis (Software-Verifikation) - zur erkennen ist eine innere Struktur, die das Problemlösen einfacher macht.
Reale Eingabe aus der Praxis (Software-Verifikation) - zur erkennen ist eine innere Struktur, die das Problemlösen einfacher macht.